
The centroid of an area is the geometrical center, i.e. the average of all of the points in an area. It is always the same, regardless of how you turn the shape.
It is also the center of gravity of a three dimensional object.
Basic Shapes
The centroids of common shapes are shown below:
| Shape | Centroid |
|---|---|
| Square/Rectangle | 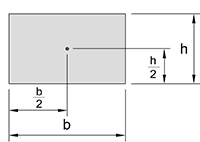 |
| Right-Angle Triangle | 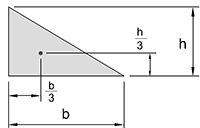 |
| Triangle | 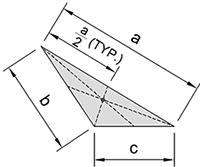 |
| Semi-circle | 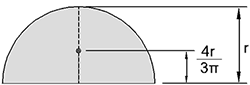 |
| Quarter-circle | 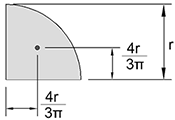 |
Multiple Shapes
Most complex real-world geometry can be estimated by approximating from a hybrid of the basic shapes. For two shapes:
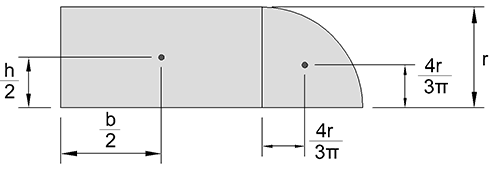
For example, with an area that looks like this:
The centroid of the shape, from the bottom left corner, is:






Leave a Reply